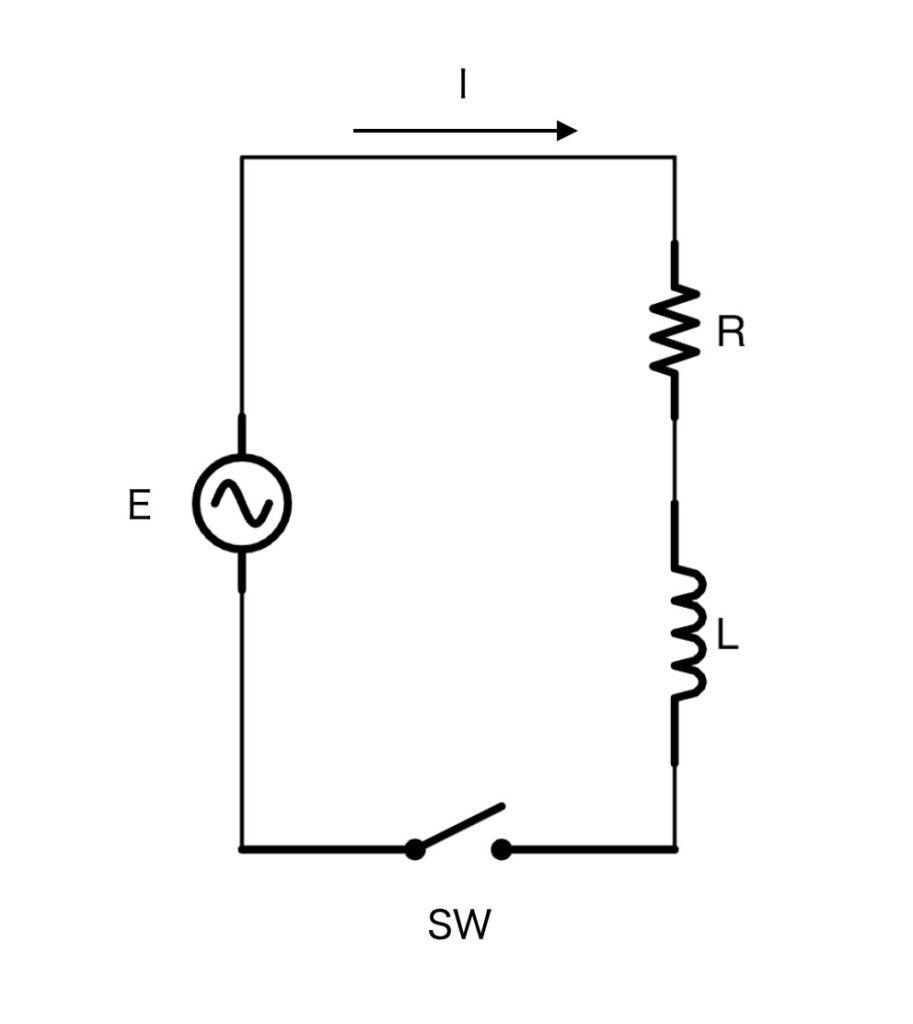
fig.1 RL series circuit(Alternating current)

Now, let’s consider an RL series circuit as shown in Figure 1, assume the AC power source is E, and think about how to find the current I that flows t seconds after turning on the switch.

Now, in the circuit of Figure 1, the following circuit equation holds true

$$RI+L\frac{dI}{dt}=E_m\sin\omega t\hspace{50pt}(1)$$

$$RI+L\frac{dI}{dt}=E_m\sin\omega t=f(t)$$

$$F(s)=\mathcal{L}f(t)$$

Laplace transform both sides of equation (1)

$$RI(s)+L\{sI(s)-I(0)\}=E_m \frac{\omega}{s^2+\omega^2}$$

If the initial value of current I(0) is 0,

$$RI(s)+LsI(s)=E_m \frac{\omega}{s^2+\omega^2}\hspace{50pt}(2)$$

Solving equation (2) for I(s), we get

$$I(s)=\frac{\omega E_m}{(R+Ls)(s^2+\omega^2)}\hspace{50pt}(3)$$

Transform the equation

$$I(s)=\frac{\frac{\omega E_m}{L}}{(s+\frac{R}{L})(s^2+\omega^2)}$$

$$$$

$$\frac{L}{\omega E_m}I(s)=\frac{1}{(s+\frac{R}{L})(s^2+\omega^2)}\hspace{50pt}$$

$$$$

$$\frac{L}{\omega E_m}I(s)=\frac{1}{(s+\frac{R}{L})(s+j\omega)(s-j\omega)}\hspace{50pt}(4)$$

Here, we create equation (5) to decompose the right-hand side of equation (4) into partial fractions.

$$\frac{1}{(s+\frac{R}{L})(s+j\omega)(s-j\omega)}=\frac{\alpha}{s+\frac{R}{L}}+\frac{\beta}{s+j\omega}+\frac{\gamma}{s-j\omega}\hspace{50pt}(5)$$

$$$$

$$=\frac{\alpha(s+j\omega)(s-j\omega)+\beta(s+\frac{R}{L})(s-j\omega)+\gamma(s+\frac{R}{L})(s+j\omega)}{(s+\frac{R}{L})(s+j\omega)(s-j\omega)}\hspace{30pt}(6)$$

$$$$

Now that the denominators are aligned, the numerator values ​​only need to match, so the condition to find from equations (5) and (6) is equation (7).

$$1=\alpha(s+j\omega)(s-j\omega)+\beta(s+\frac{R}{L})(s-j\omega)+\gamma(s+\frac{R}{L})(s+j\omega)\hspace{50pt}(7)$$

$$$$

To find α, β, and γ, substitute appropriate values ​​for s in equation (7). For simplicity, let R/L=X.

①Substituting s=-jω

$$1=-2j\omega \beta(X-j\omega)\hspace{50pt}$$

$$\beta=-\frac{1}{2j\omega(X-j\omega)}\hspace{50pt}$$

Now

$$Z=X-j\omega \hspace{50pt}$$

$$Z=|Z|e^{j\varphi}\hspace{50pt}$$

Then（see figure 2）

$$\beta=-\frac{1}{2j\omega \sqrt{X^2+\omega^2}e^{-j\varphi}}\hspace{50pt}$$

$$=-\frac{e^{j\varphi}}{2j\omega \sqrt{X^2+\omega^2}}\hspace{50pt}(8)$$

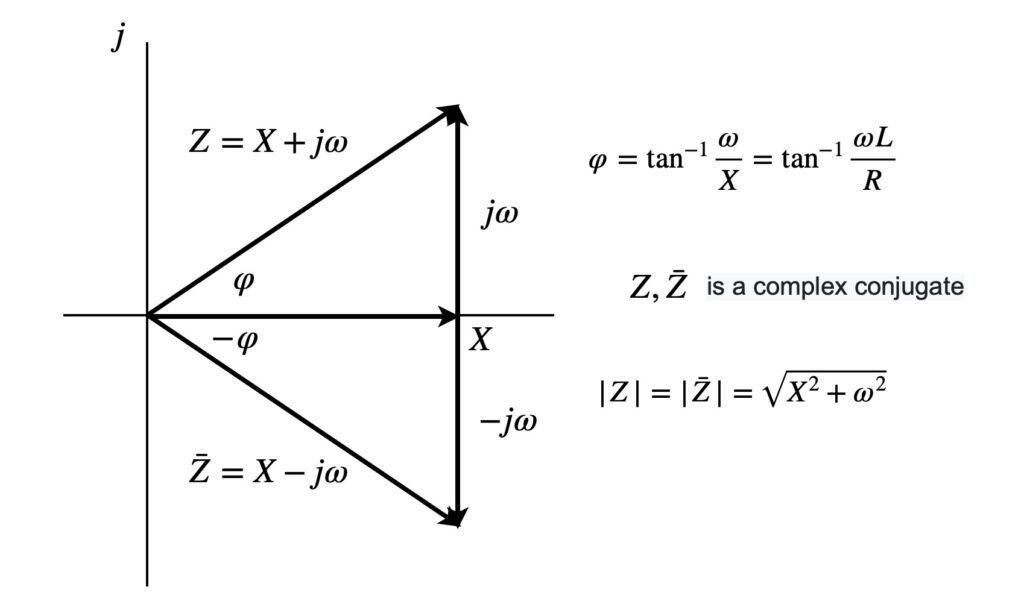
fig.2 complex conjugate

②Substituting s=jω

$$1=2j\omega \gamma(X+j\omega)\hspace{50pt}$$

$$\gamma=\frac{1}{2j\omega(X+j\omega)}\hspace{50pt}$$

$$=\frac{1}{2j\omega \sqrt{X^2+\omega^2}e^{j\varphi}}\hspace{50pt}$$

$$=\frac{e^{-j\varphi}}{2j\omega \sqrt{X^2+\omega^2}}\hspace{50pt}(9)$$

③Substituting s=-R/L

$$1=\alpha(-X+j\omega)(-X-j\omega)\hspace{50pt}$$

$$\alpha=\frac{1}{(X-j\omega)(X+j\omega)}\hspace{50pt}$$

$$=\frac{1}{X^2+\omega^2}\hspace{50pt}(10)$$

Substituting the obtained α, β, and γ into equation (5), we get

$$\frac{L}{\omega E_m}I(s)=\frac{1}{(X^2+\omega^2)(s+X)}-\frac{e^{j\varphi}}{2j\omega \sqrt{X^2+\omega^2}(s+j\omega)}+\frac{e^{-j\varphi}}{2j\omega \sqrt{X^2+\omega^2}(s-j\omega)}$$

$$$$

$$I(s)=\frac{\omega E_m}{L\sqrt{X^2+\omega^2}}\biggl\{\frac{1}{\sqrt{X^2+\omega^2}(s+X)}-\frac{e^{j\varphi}}{2j\omega(s+j\omega)}+\frac{e^{-j\varphi}}{2j\omega(s-j\omega)}\biggr\}\hspace{20pt}(11)$$

$$$$

If we inversely transform Laplace on both sides of equation (11), we get

$$\mathcal{L^{-1}}I(s)=\frac{\omega E_m}{L\sqrt{X^2+\omega^2}}\biggl\{\frac{e^{-Xt}}{\sqrt{X^2+\omega^2}}-\frac{e^{j\varphi}e^{-j\omega t}}{2j\omega}+\frac{e^{-j\varphi}e^{j\omega t}}{2j\omega}\biggr\}$$

$$$$

$$=\frac{\omega E_m}{L\sqrt{X^2+\omega^2}}\biggl\{\frac{e^{-Xt}}{\sqrt{X^2+\omega^2}}+\frac{e^{j(\omega t-\varphi)}-e^{-j(\omega t-\varphi)}}{2j\omega}\biggr\}\hspace{30pt}(12)$$

$$$$

From Euler’s formula

$$e^{j(\omega t-\varphi)}=\cos(\omega t-\varphi)+j\sin(\omega t-\varphi)\hspace{30pt}(13)$$

$$e^{-j(\omega t-\varphi)}=\cos(\omega t-\varphi)-j\sin(\omega t-\varphi)\hspace{30pt}(14)$$

$$※\cos(-\theta)=\cos\theta,\hspace{10pt}\sin(-\theta)=-\sin\theta$$

Calculating (13)+(14)

$$e^{j(\omega t-\varphi)}+e^{-j(\omega t-\varphi)}=2\cos(\omega t-\varphi)$$

$$\cos(\omega t-\varphi)=\frac{e^{j(\omega t-\varphi)}+e^{-j(\omega t-\varphi)}}{2}\hspace{50pt}(15)$$

Calculating (13)-(14)

$$e^{j(\omega t-\varphi)}-e^{-j(\omega t-\varphi)}=2j\sin(\omega t-\varphi)$$

$$\sin(\omega t-\varphi)=\frac{e^{j(\omega t-\varphi)}-e^{-j(\omega t-\varphi)}}{2j}\hspace{50pt}(16)$$

From equation (16), equation (12) becomes

$$I(t)=\frac{\omega E_m}{L\sqrt{X^2+\omega^2}}\biggl\{\frac{e^{-Xt}}{\sqrt{X^2+\omega^2}}+\frac{\sin(\omega t-\varphi)}{\omega}\biggr\}\hspace{30pt}(17)$$

$$$$

$$=\frac{\omega E_m}{L\sqrt{\frac{R^2}{L^2}+\omega^2}}\biggl\{\frac{e^{-\frac{R}{L}t}}{\sqrt{\frac{R^2}{L^2}+\omega^2}}+\frac{\sin(\omega t-\varphi)}{\omega}\biggr\}\hspace{30pt}(18)$$

$$$$

$$=\frac{E_m}{\sqrt{R^2+\omega^2L^2}}\biggl\{\frac{\omega L}{\sqrt{R^2+\omega^2L^2}}e^{-\frac{R}{L}t}+\sin(\omega t-\varphi)\biggr\}$$

$$$$

$$=\frac{E_m}{\sqrt{R^2+\omega^2L^2}}\biggl\{\sin(\omega t-\varphi)+e^{-\frac{R}{L}t}\sin\varphi\biggr\}\hspace{30pt}(19)$$

The first term in equation (19) is the current value that flows in a steady state, and the second term with an exponential function is the transient current value that flows at the moment the switch is turned on. Become.