ニュートン法とは、平方根を求める方法の一つです。この記事では、ニュートン法を使ってどのように平方根を求めるのか、考えた事をまとめました。

まず、平方根を求めたい数をkとしましょう。kの平方根をxとすると、次のように書くことができます。

$$x=\sqrt{k}$$

この式を等式変形します（両辺を２乗して、kを左辺に移項します）

$$x^2=k\\x^2-k=0$$

ここで

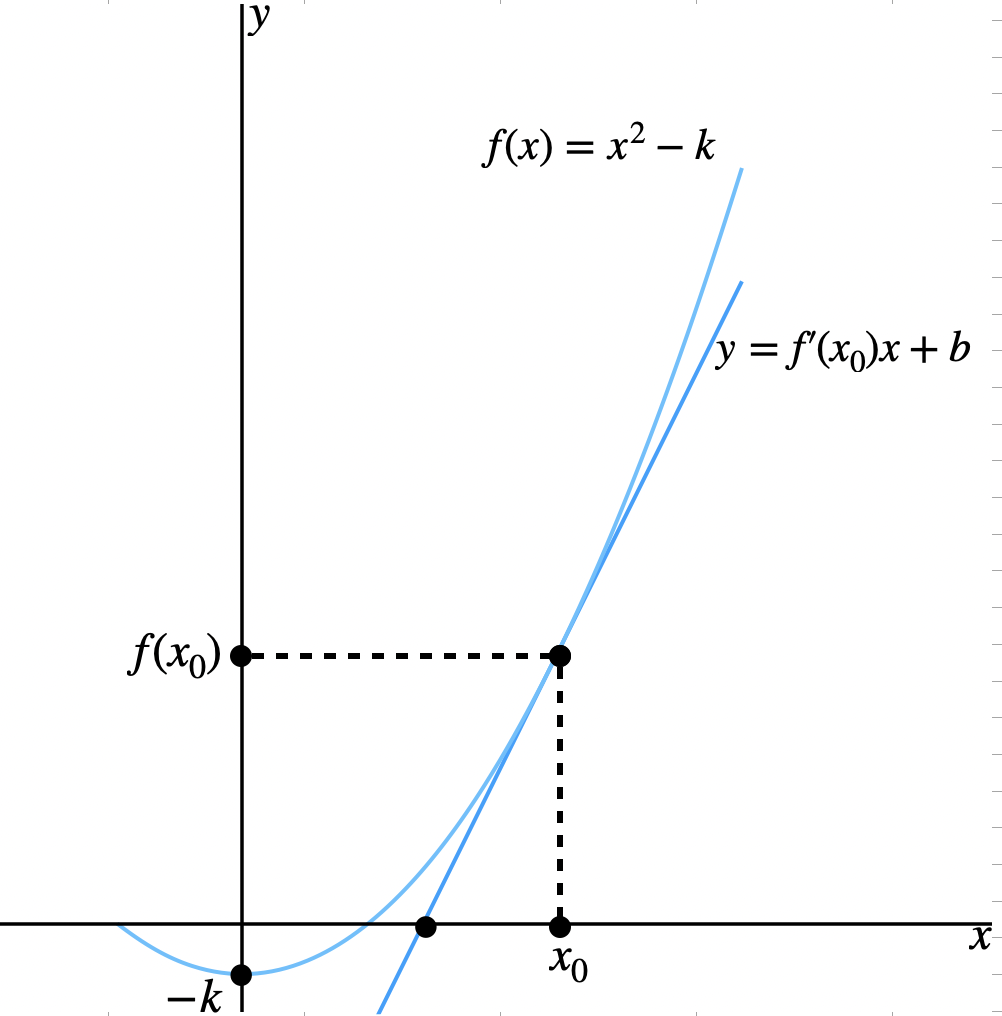
$$f(x)=x^2-k$$として、f(x)をグラフに描いてみましょう。グラフは図１のような形になります。

求めたいkの平方根は

$$x^2-k=0$$を満たすxの値と言うことになりますね。

$$グラフでは、f(x)=0になる点のxが求めたいkの平方根と言うことになります。$$

次に、グラフ上で適当な座標を考え、$$そのx座標をx_0とすると、y座標はf(x_0)と書くことができます\\(x_0,f(x_0))における接線の方程式は次のように書くことができます。$$

$$y=f'(x_0)x+b$$

この接線の方程式の切片bを求めるために、座標

$$x=x_0,y=f(x_0)$$

を代入すると

$$f(x_0)=f'(x_0)x_0+b$$

等式変形して

$$b=f(x_0)-f'(x_0)x_0$$

そうすると接線の方程式は

$$y=f'(x_0)x+f(x_0)-f'(x_0)x_0$$

この接線とx軸との交点のy座標は0なので

y=0を代入し、この点のx座標を

$$x_1$$

とすると（図３）

$$0=f'(x_0)x_1+f(x_0)-f'(x_0)x_0$$

等式変形して

$$0=x_1+ \frac{f(x_0)}{f'(x_0)}-x_0\\x_1=x_0-\frac{f(x_0)}{f'(x_0)}$$

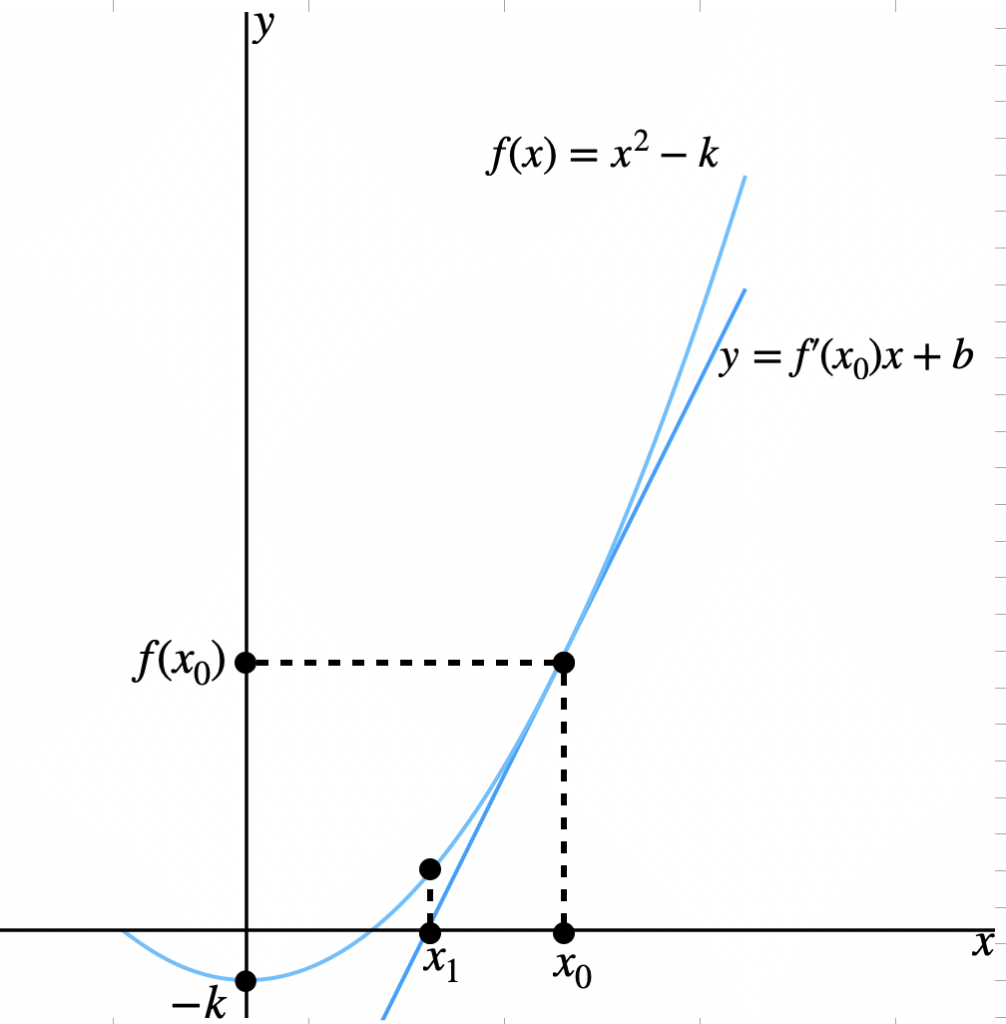
ここで、$$x_1を最初のx_0と同じように考えれば$$

同様にして

$$x_2=x_1-\frac{f(x_1)}{f'(x_1)}$$

$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$

計算を繰り返すことにより、所望の平方根に近い値を求めることができます。

（鋭意製作中）