図1のようなRL直列回路を考え、直流電源をE、t秒後に回路に流れる電流をIとすると、以下の式が成り立ちます。

$$E=RI+L\frac{dI}{dt}\hspace{50pt}(1)$$

電流Iを求めるために、(1)式の微分方程式を解きますが、この記事では、ラプラス変換を用いて微分方程式の解を求める方法を考えてみます。

ラプラス変換とは以下の式で表され、（t>0、sは複素数）

$$F(s)=\int_{0}^{\infty}e^{-st}f(t)dt$$

$$\mathcal{L}f(t)=F(s)$$

の様に表記します。

電気回路では、このラプラス変換を用いて、元の微分方程式を複素数sの領域に変換した後、sの領域で解を求め、求めた解をラプラス逆変換によりtの領域に戻すことで微分方程式の解を求めます。普通に微分方程式を解くよりも計算が簡単になるメリットがあります。

といっても、この毎回この積分を計算する必要はなく、予めわかっているラプラス変換及び逆変換の公式を用いて簡単に計算が出来ます。

今、図1の回路において

$$E=RI+L\frac{dI}{dt}=f(t)\hspace{50pt}(2)$$

と置いてf(t)のラプラス変換を

$$\mathcal{L}f(t)=I(s)$$

とします。(2)式の両辺をラプラス変換すると

$$\frac{1}{s}E=RI(s)+L\{sI(s)-I(0)\}\hspace{50pt}(3)$$

t=0における電流I(0)=0なので、(3)式は

$$\frac{1}{s}E=RI(s)+LsI(s)\hspace{50pt}(4)$$

$$I(s)=\frac{E}{(R+Ls)s}\hspace{70pt}$$

$$=\frac{\frac{E}{L}}{(\frac{R}{L}+s)s}\hspace{50pt}(5)$$

ここで、ラプラス逆変換を容易にするために、(5)式を部分分数分解により変形します。今、

$$I(s)=\frac{\frac{E}{L}}{(\frac{R}{L}+s)s}=\frac{a}{\frac{R}{L}+s}+\frac{b}{s}\hspace{50pt}(6)$$

とすると

$$\frac{\frac{E}{L}}{(\frac{R}{L}+s)s}=\frac{as+b(\frac{R}{L}+s)}{(\frac{R}{L}+s)s}\hspace{50pt}(7)$$

(7)式が恒等的に成り立つためには

$$\frac{E}{L}=as+b(\frac{R}{L}+s)\hspace{50pt}(8)$$

であれば良いので(8)式を変形して

$$\frac{E}{L}=as+b\frac{R}{L}+bs$$

$$\frac{E}{L}=(a+b)s+b\frac{R}{L}$$

この式が成り立つためには

$$a+b=0,\hspace{10pt}b\frac{R}{L}=\frac{E}{L}\hspace{50pt}(9)$$

であれば良いので、(9)式から

$$a=-\frac{E}{R},\hspace{10pt}b=\frac{E}{R}$$

ここで求めたa,bを(6)式に代入すると

$$I(s)=\frac{-\frac{E}{R}}{\frac{R}{L}+s}+\frac{\frac{E}{R}}{s}\hspace{50pt}(10)$$

$$=\frac{E}{R}\frac{1}{s}-\frac{E}{R}\frac{1}{\{s-(-\frac{R}{L})\}}$$

ラプラス逆変換の公式

$$\mathcal{L^{-1}}\frac{1}{s}=1,\hspace{10pt}\mathcal{L^{-1}}\frac{1}{s-a}=e^{at}$$

より(10)式は

$$\mathcal{L^{-1}}I(s)=\frac{E}{R}-\frac{E}{R}e^{-\frac{R}{L}t}\hspace{50pt}(11)$$

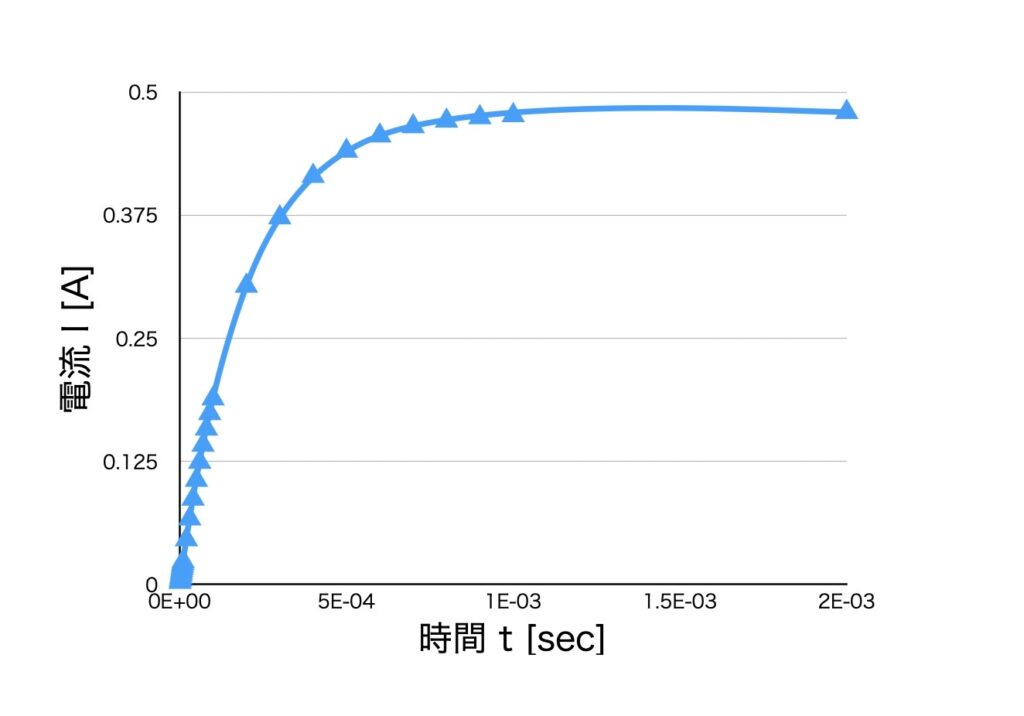
(11)式の右辺において第一項は定常状態で流れる電流値であり、第二項は電源を入れた瞬間の微小時間に流れる過渡的な電流値です。第二項はt→∞の時、0になります。