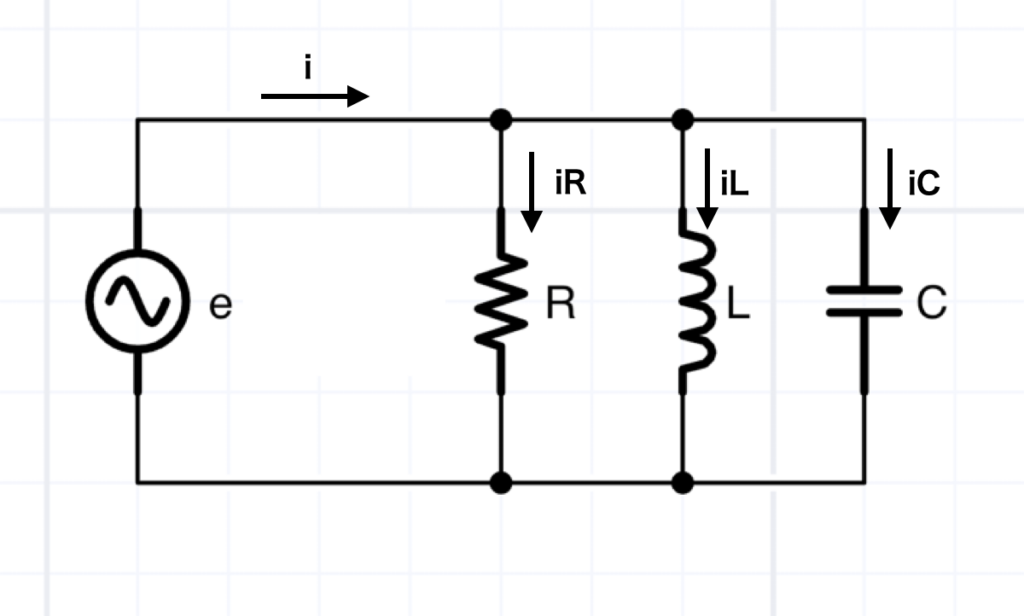
図１の様なRLC並列回路を考え、

$$e(t)=E_m\sin(\omega t-\theta)=E$$

として、回路に流れる電流iを複素数を用いた手法で求めてみましょう

今

$$e(t)=e_R=e_L=e_C$$

$$=Ri_R=L\frac{di_L}{dt}=\frac{1}{C}\int i_Cdt$$

$$=Ri_R=j\omega Li_L=\frac{i_C}{j\omega C}$$

よって

$$i_R=\frac{E}{R}$$

$$i_L=\frac{E}{j\omega L}$$

$$i_C=j\omega CE$$

今

$$i=i_R+i_L+i_C=Iと置くと$$

$$I=\frac{E}{R}+\frac{E}{j\omega L}+j\omega CE$$

$$=(\frac{1}{R}+\frac{1}{j\omega L}+j\omega C)E$$

$$=(\frac{1}{R}+\frac{j}{j}\cdot\frac{1}{j\omega L}+j\omega C)E$$

$$(\frac{1}{R}-\frac{j}{\omega L}+j\omega C)E$$

$$=\{\frac{1}{R}+j(\omega C-\frac{1}{\omega L})\}E$$

Eを指数関数表記に書き換えると

$$I=\{\frac{1}{R}+j(\omega C-\frac{1}{\omega L})\}E_m\text e^{j(\omega t-\theta)}$$

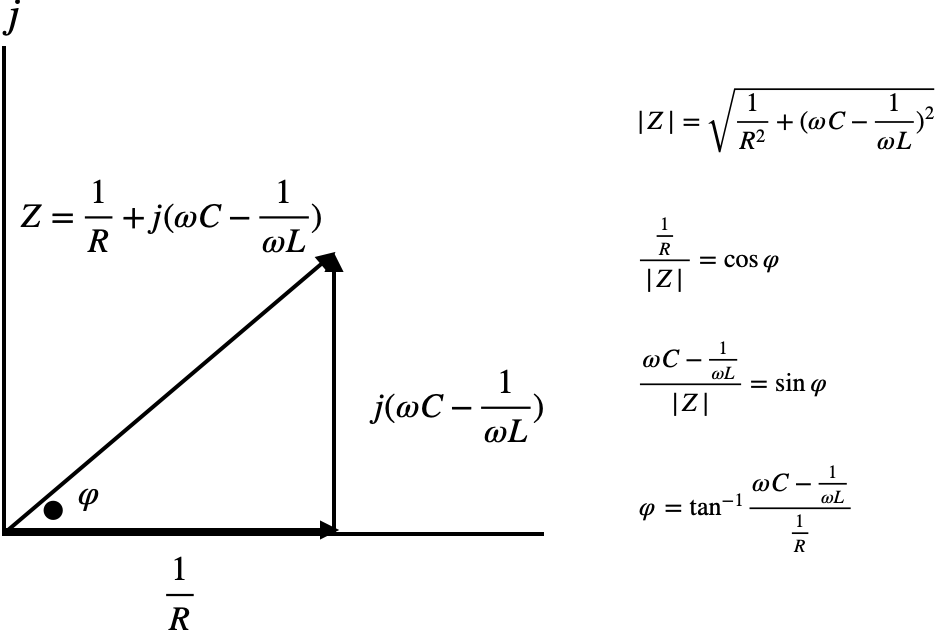
今

$$Z=\frac{1}{R}+j(\omega C-\frac{1}{\omega L})$$

とすると

$$Z=|Z|\text e^{j\varphi}$$

より

$$I=|Z|\text e^{j\varphi}E_m\text e^{j(\omega t-\theta)}$$

$$=|Z|E_m\text e^{j(\omega t-\theta+\varphi)}$$

$$=\sqrt{\frac{1}{R^2}+(\omega C-\frac{1}{\omega L})^2}E_m\text e^{j(\omega t-\theta+\varphi)}$$

三角関数表記に戻して

$$=\sqrt{\frac{1}{R^2}+(\omega C-\frac{1}{\omega L})^2}E_m\{\cos(\omega t-\theta+\varphi)+j\sin(\omega t-\theta+\varphi)\}$$

虚部のみ取ると

$$I=\sqrt{\frac{1}{R^2}+(\omega C-\frac{1}{\omega L})^2}E_m\sin(\omega t-\theta+\varphi)$$

$$\\\\$$

回路の複素インピーダンスを求めよう

今、回路に流れる電流は

$$I=(\frac{1}{R}+\frac{1}{j\omega L}+j\omega C)E$$

$$=\{\frac{1}{R}+j(\omega C-\frac{1}{\omega L})\}E$$

回路の複素インピーダンスを

$$Z_A$$

とすると

$$Z_A=\frac{E}{I}$$

$$=\frac{1}{\frac{1}{R}+j(\omega C-\frac{1}{\omega L})}$$

$$\\$$

$$=\frac{\frac{1}{R}-j(\omega C-\frac{1}{\omega L})}{\{\frac{1}{R}+j(\omega C-\frac{1}{\omega L})\}\{\frac{1}{R}-j(\omega C-\frac{1}{\omega L})\}}$$

$$\\$$

$$=\frac{\frac{1}{R}-j(\omega C-\frac{1}{\omega L})}{\frac{1}{R^2}+(\omega C-\frac{1}{\omega L})^2}$$

$$\\$$

$$=\frac{\frac{1}{R}}{\frac{1}{R^2}+(\omega C-\frac{1}{\omega L})^2}-j\frac{\omega C-\frac{1}{\omega L}}{\frac{1}{R^2}+(\omega C-\frac{1}{\omega L})^2}$$

今、簡略化のために、

$$\frac{1}{R^2}+(\omega C-\frac{1}{\omega L})^2=A$$

と置くと

$$Z_A=\frac{\frac{1}{R}}{A}-j\frac{\omega C-\frac{1}{\omega L}}{A}$$

となるので、回路のインピーダンスを

$$|Z_A|$$

とすると

$$|Z_A|=\sqrt{\frac{\frac{1}{R^2}}{A^2}+\frac{(\omega C-\frac{1}{\omega L})^2}{A^2}}$$

$$\\$$

$$=\sqrt{\frac{\frac{1}{R^2}+(\omega C-\frac{1}{\omega L})^2}{A^2}}$$

$$\\$$

$$=\sqrt{\frac{A}{A^2}}$$

$$\\$$

$$=\frac{1}{\sqrt{A}}$$

$$\\$$

$$=\frac{1}{\sqrt{\frac{1}{R^2}+(\omega C-\frac{1}{\omega L})^2}}$$