ユークリッドの互除法の使い方はシンプルですが、なぜ、その使い方で最大公約数が計算できるのか、原理について考えてみました。

はじめに、2つの自然数a,bを考え、b≦aとします。

aをbで割った時の商をq、余りをrとすると、次の様に書くことができます。

$$a=bq+r$$

いま、aとbの最大公約数をGとして、上式の両辺をGで割ると、

$$\frac{a}{G}=\frac{bq+r}{G}\\[20pt]\frac{a}{G}=\frac{bq}{G}+\frac{r}{G}$$

Gはaとbの最大公約数なので、左辺のaはGで割り切れます。則ち左辺の

$$\frac{a}{G}$$

は自然数となり、等式の性質から、右辺も自然数にならなければいけません。

そこで右辺に着目すると、bはGで割り切れて自然数になります。また、qも自然数なので、

$$\frac{bq}{G}=\frac{b}{G} \cdot q$$

の項は自然数×自然数＝自然数になります。と言うことは、

$$\frac{r}{G}$$

の項も自然数にならなければいけませんね？ したがって、rはGで割り切れることがわかります。

したがってGはa,b,rの公約数といえます。しかし、Gがbとrの最大公約数であるかは分かりません。そこでさっきの式を見ながら、もう少し考えてみましょう。

$$\frac{a}{G}=\frac{bq}{G}+\frac{r}{G}$$

bとrの最大公約数をgとすると、gはbとrの公約数の中で最も大きい値ですから、gはGと等しいか、gはGより大きくならなければなりません。則ち

$$g\geq G$$

同様に、

$$a=bq+r$$

の両辺をbとrの最大公約数gで割ると

$$\frac{a}{g}=\frac{bq}{g}+\frac{r}{g}\\[20pt]\frac{a}{g}=\frac{b}{g} \cdot q+\frac{r}{g}$$

いま、

$$\frac{b}{g},\hspace{10pt}\frac{r}{g},\hspace{10pt}q$$

の項は全て自然数ですから、右辺は自然数になります。したがって、左辺の

$$\frac{a}{g}$$

も自然数となり、aはgで割り切れることが分かります。したがって、gはa,b,rの公約数であることが分かります。ここで、先程と同様に、次の式を見ながら考えてみましょう。

$$\frac{a}{g}=\frac{bq}{g}+\frac{r}{g}$$

aとbの最大公約数Gは、aとbの公約数の中で最も大きい値ですから、Gはgと等しいか、Gはgより大きくならなければなりません。則ち

$$G\geq g$$

整理すると

$$g\geq G\hspace{5pt}且つ\hspace{5pt}G\geq g$$

となりますが、この2つの不等式を満たすには

$$G=g$$

でなければなりません。例えばg>Gの場合を考えてみましょう。仮にg=5,G=4とすると、

$$5\geq 4 $$

は成り立ちますが

$$4\geq 5$$

は成り立ちません。同様にG>gの場合、G=5,g=4とすると

$$5\geq 4$$

は成り立ちますが、

$$4\geq 5$$

は成り立ちません。したがって、G=gとなります。

まとめると、aとbの最大公約数Gは、bとrの最大公約数gと等しいことになるのです。

最大公約数の計算手順

いま、2つの自然数a、bの最大公約数を求めるためにaをbで割って余りを出し、次の様に書きます。

$$a=bq+r$$

aとbの最大公約数はbとrの最大公約数と等しいので、bをrで割って、

$$b=a_2,\hspace{5pt}r=b_2$$

とすると

$$a_2=b_2 q_2+r_2$$

$$同様にa_2とb_2の最大公約数はb_2,r_2の最大公約数と等しいので\\b_2をr_2で割って余りを出して・・を繰り返します。\\$$

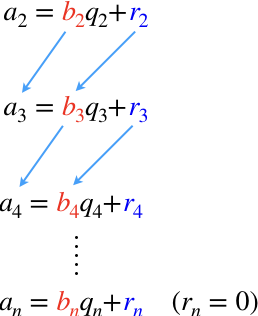
$$最終的にr_n=0になった時のb_nがaとbの最大公約数となります。$$割り算を繰り返すことにより、元の数a,bよりもずっと小さな2つの自然数を比較することで所望の最大公約数を得ることができるのです。

ユークリッドの互除法のアルゴリズムを利用した、2つの自然数の最大公約数を計算するツールもありますので、よろしければ遊んでみてください。

⇨⇨http://megro-aquarius29.com/?p=1182