マクローリン展開の基本式

$$f(x)=f(0)+f'(0)x+\frac{f^{(2)}(0)}{2!}x^2+\frac{f^{(3)}(0)}{3!}x^3+\cdot\cdot\cdot=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n$$

を利用して、身近な関数を展開してみよう！

$$\sin(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n\hspace{200pt}\\[20pt]=\sin(0)+\cos(0)x-\frac{\sin(0)}{2!}x^2-\frac{\cos(0)}{3!}x^3+\frac{\sin(0)}{4!}x^4+\frac{\cos(0)}{5!}x^5+\cdot\cdot\cdot$$

sin(0)=0なので、nが偶数の項は全て0になります。したがって

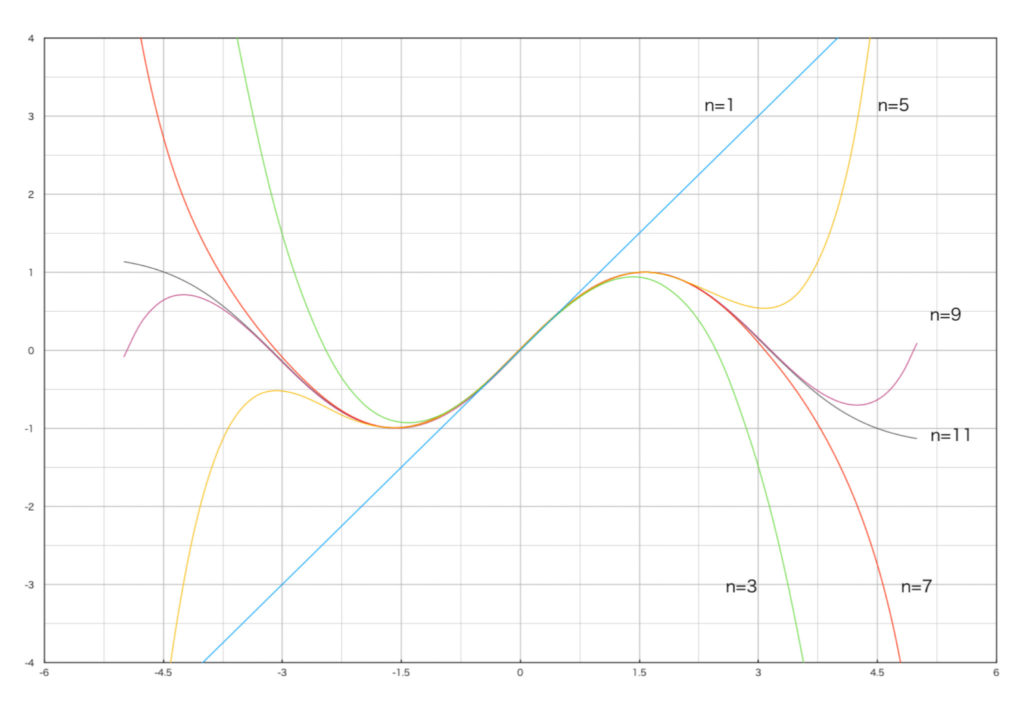
$$\sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}+\cdot\cdot\cdot=\sum_{p=0}^{\infty}(-1)^p\frac{x^{2p+1}}{(2p+1)!}$$

$$\cos(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n\hspace{200pt}\\=\cos(0)-\sin(0)x-\frac{\cos(0)}{2!}x^2+\frac{\sin(0)}{3!}x^3+\frac{\cos(0)}{4!}x^4-\frac{\sin(0)}{5!}x^5+\cdot\cdot\cdot$$

sin(0)=0なので、nが奇数の項は全て0になります。したがって

$$\cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}+\cdot\cdot\cdot=\sum_{p=0}^{\infty}(-1)^p\frac{x^{2p}}{(2p)!}$$

$$\exp(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n\hspace{200pt}\\=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdot\cdot\cdot=\sum_{p=0}^{\infty}\frac{x^p}{p!}\hspace{75pt}$$