三角形の面積を求める方法は様々ですが、ヘロンの公式をご存知でしょうか。この公式は、三角形の三辺の長さだけを使って、三角形の面積を計算できる、便利な公式です。
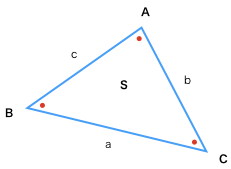
図1の様な角A,B,C、辺a,b,cをもつ三角形の面積をSとすると
$$S=\sqrt{s(s-a)(s-b)(s-c)}\hspace{20pt}(s=\frac{a+b+c}{2})$$
となり、これをヘロンの公式と呼びます。当記事では、ヘロンの公式を導出してみたいと思います。
step1 導出に必要な定理のおさらい
図1において、余弦定理より
$$\cos A=\frac{b^2+c^2-a^2}{2bc}\\[25pt]\cos B=\frac{c^2+a^2-b^2}{2ca}\\[25pt]\cos C=\frac{a^2+b^2-c^2}{2ab}$$
三角形の面積を求める公式から
$$S=\frac{1}{2}bc\cdot \sin A=\frac{1}{2}ca\cdot \sin B=\frac{1}{2}ab\cdot \sin C$$
三角比の相互関係から
$$\sin^2A+\cos^2A=1\\[25pt]\sin^2A=1-\cos^2A\\[25pt]\sin A=±\sqrt{1-\cos^2A}$$
三角形の一つの内角Aの大きさの範囲は、0<A<180[deg]です。つまり座標平面上では、第1象限と第2象限がその範囲になります。第1、2象限においてsinAの値は常に正になりますね。したがってこの場合sinA>0となるので、
$$\sin A=\sqrt{1-\cos^2A}$$
Step2
まずはじめに、
$$\sin A=\frac{\sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}}{2bc}$$
であることを導きましょう。
三角比の相互関係の式
$$\sin A=\sqrt{1-\cos^2A}\hspace{200pt}$$
に、余弦定理の公式
$$\cos A=\frac{b^2+c^2-a^2}{2bc}\hspace{200pt}$$
を代入すると、
$$\sin A=\sqrt{1-\frac{(b^2+c^2-a^2)^2}{(2bc)^2}}\hspace{300pt}\\[25pt]=\sqrt{\frac{(2bc)^2-(b^2+c^2-a^2)^2}{(2bc)^2}}\hspace{260pt}\\[25pt]=\frac{\sqrt{(2bc+b^2+c^2-a^2)(2bc-b^2-c^2+a^2)}}{2bc}\hspace{200pt}\\[25pt]=\frac{\sqrt{\{(b+c)^2-a^2\}\{-(b^2-2bc+c^2)+a^2\}}}{2bc}\hspace{200pt}\\[25pt]=\frac{\sqrt{\{(b+c)^2-a^2\}\{a^2-(b-c)^2\}}}{2bc}\hspace{240pt}\\[25pt]=\frac{\sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}}{2bc}\hspace{190pt}$$
Step3
三角形の面積を求める公式から
$$S=\frac{1}{2}bc\cdot \sin A\\[25pt]∴S=\frac{1}{2}bc\cdot\frac{\sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}}{2bc}\\[25pt]=\frac{\sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}}{4}\\[25pt]=\sqrt{\frac{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}{16}}\\[25pt]\hspace{30pt}=\sqrt{\frac{(b+c+a)}{2}\cdot\frac{(b+c-a)}{2}\cdot\frac{(a+b-c)}{2}\cdot\frac{(a-b+c)}{2}}$$いま$$s=\frac{a+b+c}{2}$$と置くと(sは小文字)、
$$s-a=\frac{a+b+c}{2}-a\\[25pt]\hspace{20pt}=\frac{a+b+c-2a}{2}\\[25pt]=\frac{b+c-a}{2}$$同様に
$$s-b=\frac{a+b+c}{2}-b\\[25pt]\hspace{20pt}=\frac{a+b+c-2b}{2}\\[25pt]=\frac{a-b+c}{2}$$同様に
$$s-c=\frac{a+b+c}{2}-c\\[25pt]\hspace{20pt}=\frac{a+b+c-2c}{2}\\[25pt]=\frac{a+b-c}{2}$$
したがって
$$S=\sqrt{s(s-a)(s-b)(s-c)}\hspace{20pt}(s=\frac{a+b+c}{2})$$
と、このようにヘロンの公式を導出することができます。
この公式は、1世紀頃にアレクサンドリアで活動していたギリシア人数学者のヘロンによって証明されたそうです。
ヘロンの公式は土地の概面積を算出する場合に使えます。例えば土地の面積がn角形の場合、n角形は(n-2)個の三角形に分割することができます。其々の三角形の三辺の長さを測定すれば、多角形の面積は三角形の面積の和で表されます。
