因数分解の公式

$$x^3+y^3=(x+y)(x^2-xy+y^2)\\[10pt]x^3-y^3=(x-y)(x^2+xy+y^2)$$

を、因数定理を利用して導出できます。

剰余の定理と因数定理についておさらい

はじめに具体的な数字で考えてみましょう。

例えば10を6で割った場合、商は1、余りは4です。これは次の様に書くこともできます。$$10=6\times1+4$$

同様に、整式P(x)をx-αで割った時の商をQ(x)、余りをRとすると$$P(x)=(x-\alpha)Q(x)+R\hspace{50pt}(1)$$

と書くことができます。

ちょっと補足・・・整式とは

$$例えば2x^3+5x^2-4x+6の様な式を整式と呼び、\\[5pt]整式Pがxについての整式であることをはっきり示したい場合に\\[5pt]P(x)=2x^3+5x^2-4x+6の様に表記します。\\[5pt]整式P(x)に特定の値αを代入した時の整式Pの値をP(α)と書きます。\\[5pt]例）\alpha=1の時、P(1)=2\cdot1^3+5\cdot1^2-4\cdot1+6=9$$

さて、(1)式においてx=αの場合を考えると、

$$P(\alpha)=(\alpha-\alpha)Q(x)+R=R$$

となり、余りの項Rのみが残ります。つまり、P(x)をx-αで割った時の余りRを知りたければ、

P(x)にαを代入した時の値を求めれば良いことになります。これが剰余の定理です。

次に、整式P(x)にαを代入した時の値が0の時、即ちP(α)=0の場合を考えると、

$$P(\alpha)=(\alpha-\alpha)Q(x)+R=0\\[10pt]∴R=0$$

となり、P(x)はx-αで割り切れるということです。

$$P(α)=0ならば整式P(x)はx-αで割り切れる。$$

これが因数定理です。

いま

$$P(x)=x^3+y^3とすると\\P(-y)=(-y)^3+y^3=0$$

となり

$$P(x)=x^3+y^3はx-(-y)=x+yで割り切れます。$$

整式の除法を用いて計算すると

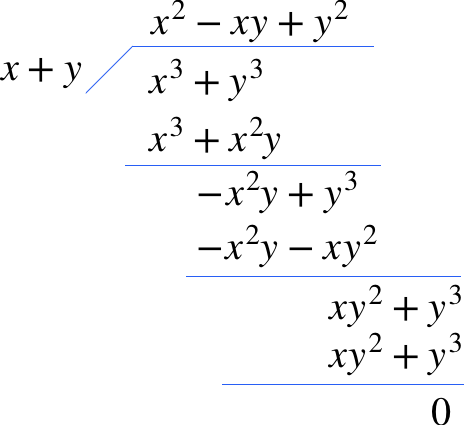
となり$$x^3+y^3はx+yで割り切れることが確認できました。$$

即ち$$x^3+y^3=(x+y)(x^2-xy+y^2)の公式が導かれました。$$

同様にして

$$x^3-y^3$$の因数分解公式も導くことができます。

$$P(x)=x^3-y^3とすると\\P(y)=y^3-y^3=0となり$$

$$x^3-y^3はx-yで割り切れます。$$

整式の除法を用いて計算すると

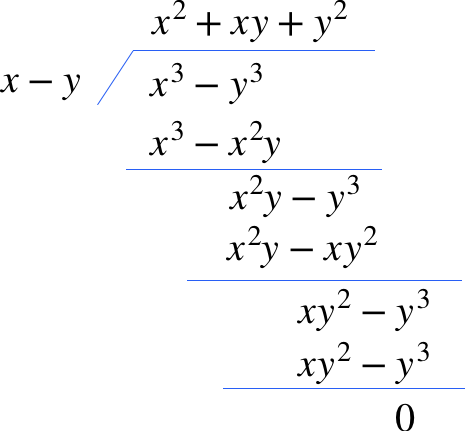
となり、$$x^3-y^3はx-yで割り切れることが確認できました。$$

即ち$$x^3-y^3=(x-y)(x^2+xy+y^2)$$となることが導かれました。

この因数定理は高次方程式を解く際にも用いられ、内容を理解して使いこなすことができれば、便利なツールです。